# 点到线段的距离
# 两种情况
首先要判断点 到直线 的投影是否落在线段 上。
若落在线段内,即 和 为锐角,则距离为点到直线 的距离
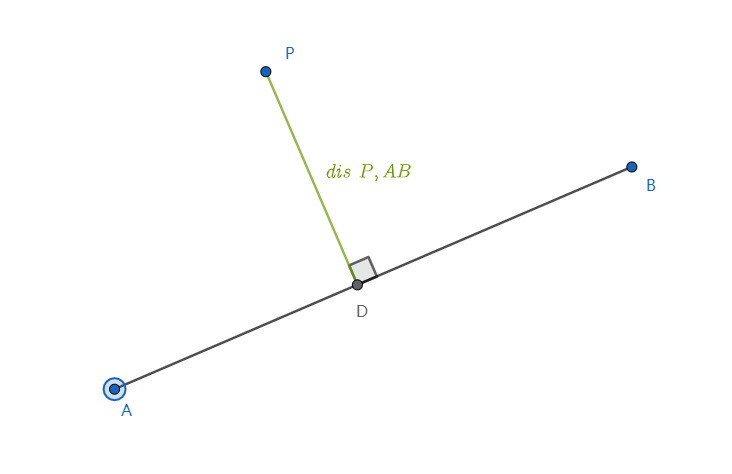
若落在线段外,即 或 为钝角,则距离为点到线段 的最近端点的距离
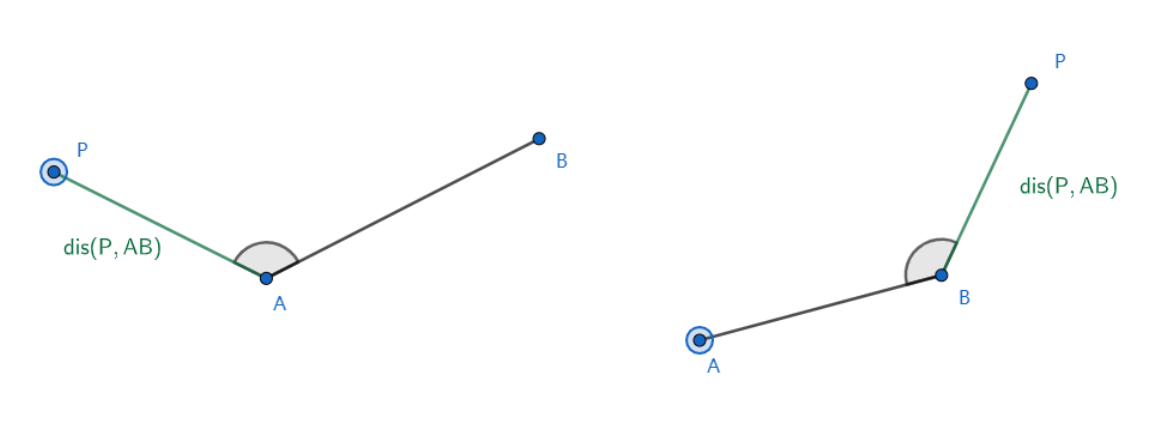
# 如何判断垂足是否落在线段上?
有两种做法。
第一种根据角度判断,若、 均为锐角,则为情况一,否则为情况二。
这里可以利用向量的点积运算。
我们知道
那么根据 和 的正负即可判断是否锐角。
第二种根据投影长度判断。若投影 与线段 的长度之比在 之间,表明垂足落在线段 内。
这里依然利用点积运算的式子
AD 与 AB 之比即为
我们检验这个值是否落在 即可。
# 计算距离
对于情况一,点到直线的距离,可以使用三角形面积推算。
对于情况二,简单对 P 到 AB 两点距离取最小值即可。
# 附代码
inline double sqr(const double &x){// 平方 | |
return x*x; | |
} | |
struct P{ | |
double x,y; | |
double len()const{// 模长 | |
return sqrt(x*x+y*y); | |
} | |
double dot(const P &rv)const{// 点乘 | |
return x*rv.x+y*rv.y; | |
} | |
double cross(const P &rv)const{// 叉乘 | |
return x*rv.y-y*rv.x; | |
} | |
double dis(const P &rv)const{// 两点距离 | |
return sqrt(sqr(x-rv.x)+sqr(y-rv.y)); | |
} | |
P operator - (const P &rv)const{// 取向量 | |
return {x-rv.x,y-rv.y}; | |
} | |
}; | |
struct Seg{ | |
P a,b; | |
P vec; | |
Seg()=default; | |
Seg(const P &a,const P &b):a(a),b(b),vec(b-a){} | |
double dis(const P &p){// 点到线段的距离 | |
double d=(p-a).dot(vec)/sqr(vec.len()); | |
if(d>0 && d<1) | |
return fabs((p-a).cross(vec)/vec.len()); | |
return std::min(p.dis(a),p.dis(b)); | |
} | |
}; |